1. 数列极限的定义
极限 <=> 无限的接近
定义对于一个无穷数列,如果存在一个常数,无论预先指定多么小的正数,都能在数列中找到一项,使得这一项后面所有的项与的差的绝对值都小于(即当时,恒成立),就把常数叫做数列{}的极限,记作
上述定义可以简述为 任意给定,如果总存在自然数,使得当时,不等式恒成立,就说数列{}的极限是。 这个定义还可以用记号表示为

2. 极限的四则运算
运用法则时应注意之点,对数列和函数极限是一样的. 以下是数列极限的四则运算法则: 如果 , , 那么.
在使用它们时,要特别注意各个法则成立的条件.
- 法则(1) , (2) , (3)可以推广到有限个数列的情形.
- 法则(1) , (2) , (3)的极限必须存在
- 在运用法则(3)时,必须注意分母的极限不能为零.
3. 无穷等比数列的各项和
无穷等比数列的和
于是得到
如果
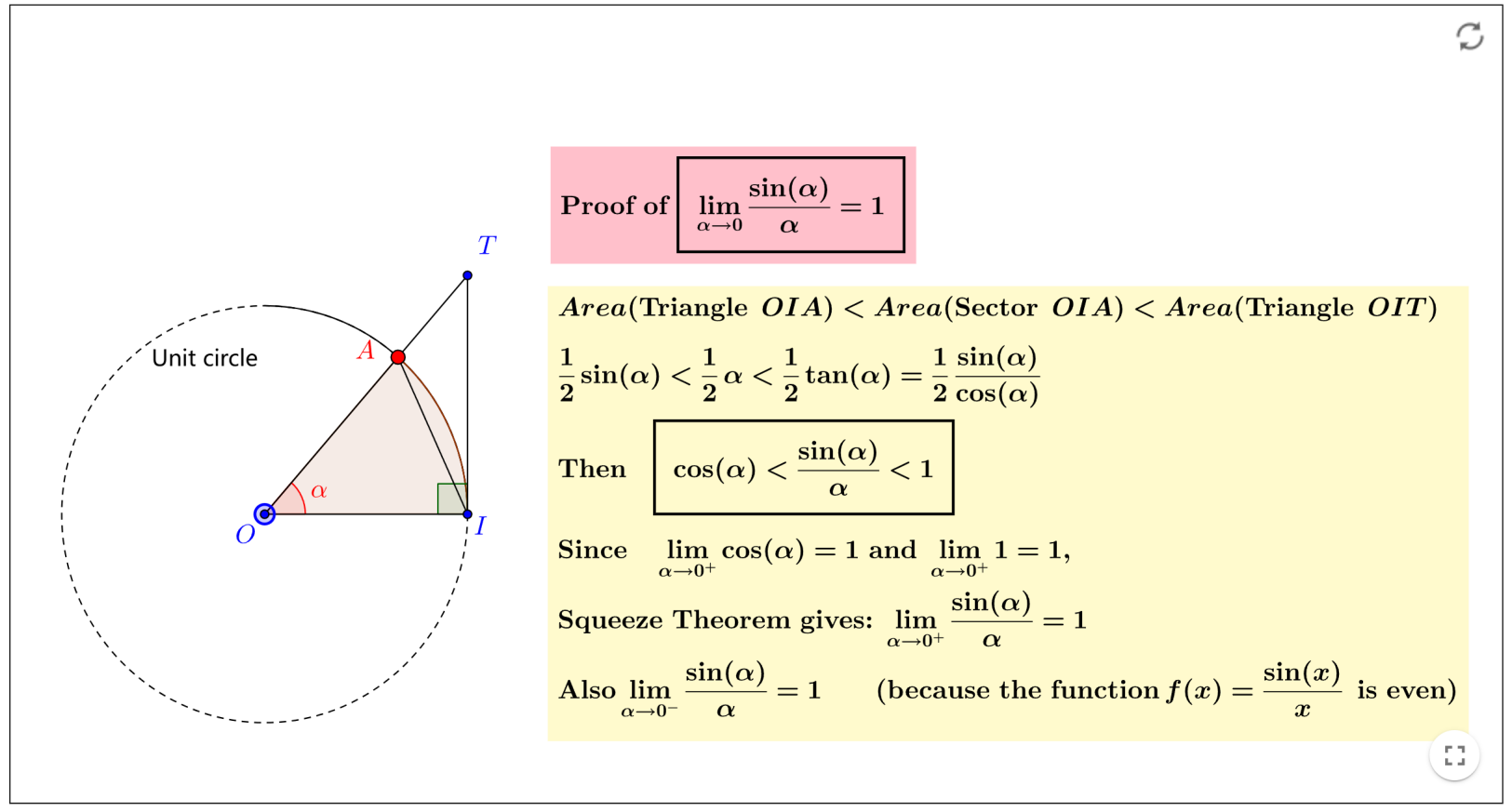
4. 两个重要极限
5. 函数的连续性
连续 <=> 没有断裂,可以一笔画成
设函数 在点 的某个邻域内有定义,如果满足以下条件:
则称函数 在点 处连续。
5.1 连续性的三个条件
函数 在点 处连续,必须同时满足以下三个条件:
- 有定义: 存在(函数在 点有定义)
- 有极限: 存在
- 相等:
如果上述三个条件中至少有一个不满足,则函数在点 处不连续,称 为函数的间断点。
5.2 增量形式定义
设函数 在点 的某个邻域内有定义,如果当自变量的增量 趋于零时,对应的函数增量 也趋于零,即:
则称函数 在点 处连续。
5.3 单侧连续性
如果 ,则称函数 在点 处左连续。
如果 ,则称函数 在点 处右连续。
函数 在点 处连续的充分必要条件是:函数在该点既左连续又右连续。
5.4 区间上的连续性
开区间 上的连续性:如果函数 在开区间 内每一点都连续,则称 在 内连续。
闭区间 上的连续性:如果函数 在开区间 内连续,且在左端点 处右连续,在右端点 处左连续,则称 在闭区间 上连续。
5.5 连续函数的性质
四则运算性质:如果函数 和 在点 处连续,则它们的和、差、积、商(分母不为零)也在点 处连续。
复合函数性质:如果函数 在点 处连续,且函数 在点 处连续,则复合函数 在点 处连续。
反函数性质:如果函数 在区间 上单调且连续,则其反函数 也在对应的区间上单调且连续。
5.6 初等函数的连续性
所有基本初等函数(幂函数、指数函数、对数函数、三角函数、反三角函数等)在其定义域内都是连续的。
由基本初等函数经过有限次四则运算和复合运算得到的初等函数,在其定义区间内都是连续的。
5.7 间断点的分类
如果 存在,但不等于 或者 无定义,则称 为可去间断点。
如果 不存在,则称 为第二类间断点。
5.8 例题分析
讨论函数 在点 处的连续性。
解:
- 计算函数值:
- 计算左极限:
- 计算右极限:
- 因为左极限 右极限,所以极限不存在。
结论:函数在 处不连续,这是一个跳跃间断点(属于第一类间断点)。
讨论函数 在点 处的连续性。
解:
- 函数在 处无定义
- 计算极限:(重要极限)
- 极限存在但函数无定义
结论: 是一个可去间断点。如果补充定义 ,则函数在 处连续。函数 fx 在点 x0处,连续