LCA在线算法
LCA: 求树上两个点最近公共祖先的算法
原理
在讲解之前,我们先想两个问题,这两个问题也是LCA在线算法的核心:
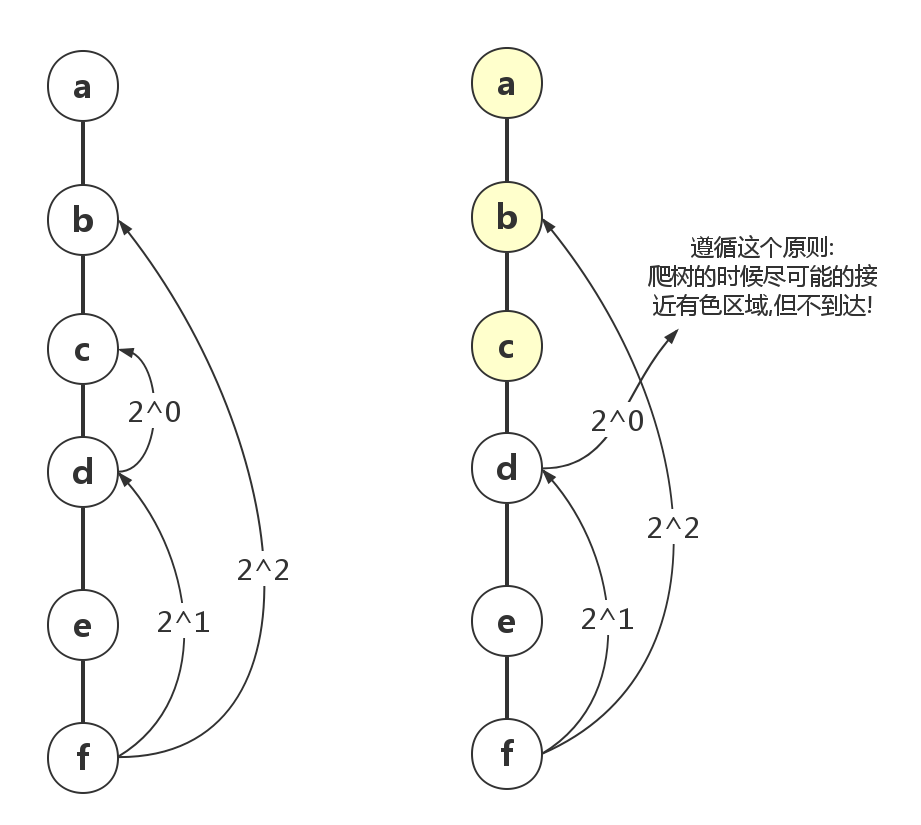
问题1:
如上图左部,f点有一个超能力–超能爬树:可以快速查看或爬到$2^j$远的结点上,例如爬到$2^0$远的结点就是1,$2^2$远的结点是b,每一次f到达某个点都可以知道是比要到的点高了还是低了.那如何结点f如何快速的到达点c? 结点f如何快速的到达它上面的任意点?
想一想:折半查找应该算是最快的查找方法之一,$Nlog(n)$的时间复杂度.
那我们按下面的方法来找:
如上图左部的步骤:
- f先到最远的点,距离$2^2$远的点,也就是b看看,发现高了
- 因为了高了,那f到距离$2^1$远的点(d)看看,发现在低了
- 因为低了,说明要到达的点c在点d的上面,那f就爬到点d
- f到距离$2^0$远的点c看看,发现就是这个点,f爬到这个.算法结束.
更抽象的步骤:
- f先达到最高的地方,假如是$2^k$远的点
- 如果高了,那要找的点在下面,到$2^(k-1)$点,也就是到达最远的地方的一半远看看
- 如果低了,那说明要找的点在上面,那就先爬到个点,然后到达$2^(k-1)$远的地方看看
- 现在f已经到达了某个点,那f接着到现在位置的$2^(k-2)$远的地方看看
- 如果高了,那说明要找的点在下面(想一想这个时候要找的点在哪个区间),那到现在$2^(k-3)$远的地方看看
- 如果低了,那说明要找的点在上面,那就先爬到这个点,然后到达$2^(k-3)$的地方看看
- 经过上面的不停重复,那最后$k=0$,这个时候停下的位置就是f想要到达的点
问题2
看上图右部,f依然有它的超能爬树这个能力,现在最上面的点a,b,c是有色的点,f不能到达有色的点,但是它想到
离有色剖分最近的点怎么做?
如上图右部的步骤:
- f先到最远的点,距离$2^2$远的点,也就是b看看,发现是有色,不能到
- 那f到距离$2^1$远的点,也就是d看看,发现无色
- 因为d是无色,那f就爬到点d,但是d上面还有可能有无色的点(想一想哪个范围是),f爬到点d
- f到距离$2^0$远的点c看看,发现是有色,不能到达,算法停止.f最后停下的地方就是最接近有色区域的点.
更抽象的步骤:
通过问题1,点f可以通过不停减少k的方式,快速到达想要到达的点,且最后$k=0$,你把有色区域想成一个点,按这
种方式,f最后一点会到达这个点,但是你加上了一个限制条件: 有色区域不能到达!.f的行为是尽可能的去,那最后f停下的
位置就是最近的位置
总结
上面的方法用一句话来形容:折半尝试,它会把结果的可能性每次缩小一半,最后$k=0$的时候只有两种可能性,要么是
自己,要么是上面一个点,所以可以得到答案.这是一中倍增思想.
转为代码
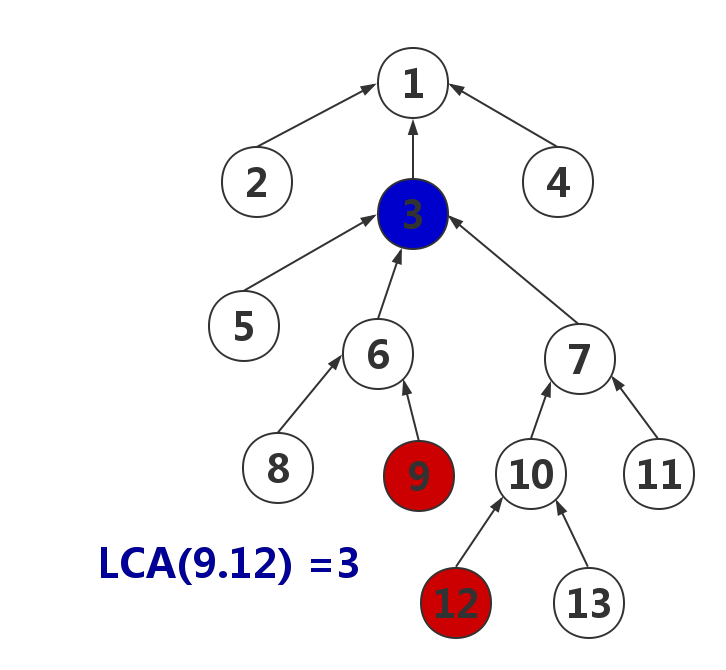
看这个图,我们分为这几个步骤来做
- 初始化,也是ST部分,求任意点i的$2^j$倍祖先:$p[i,j]$
- 把点
9和点12移到同一层,也就是找12和9同一层的祖先,得用是问题的方法 - 上面我们已经知道
LCA(9,12) == LCA(9,10), - 点1,3都是祖先,但是不知道哪个点是最近公共祖先,所心只要我们近可能的接近
祖先区域,那最近停下时候的点的父亲,就是所求.
ST 预处理
已知:点i的父亲是f[i],深度是d[i],p[i][j]表示点i的$2^j$倍祖先,那么根据DP思想,我们得到一个重要的公式:
$$p[i,j]=\left\{\begin{matrix} & father[i] &j=0 \\ & p[p[i,j-1],j-1] &j>0\end{matrix}\right.$$
那么ST代码:
int d[100] = {0};//每个点的深度
int f[100];//每个点的父亲
int p[100][100];
void st(){
int i,j;
memset(p,-1,sizeof(p));//想一想:为什么是-1
for(i=1;i<=n;i++) // n个点,dp边界
p[i,0]=f[i];
//n个点,理论最深是n,也就是最大有n-1倍祖先,我们算大一点:算成n倍祖先
// 2^j =n --->j=log(n)/log(2)
for(j=1;j<=(int)(log(n)/log(2));j++)
for(i=1;i<=n;i++)
if(p[i][j-1] != -1)// [1] p[i][j-1] != -1 表明可以用自己去更新别人,为什么要有这个判断?
p[i,j] = p[p[i,j-1],j-1];
}
两个点到同一层
/* 先判断是否 d[a] > d[b] ,如果是的话就交换一下(保证 a 的深度小于b,方便下面的操作) */
int i;
if(d[a] > d[b])
{
int tmp =a;
a=b;
b=tmp;
}
/* 转为找同层结点 d[a] <= d[b] */
/* 这种找法 能成功的原因,看折半查找原理*/
int k = (int)(log(d[b]-1)/log(2));//公式 root 点是b点d[b]-1倍祖先
for(i=k;i>=0;i--){
if(d[b]-(1<<i) >=d[a]) //1<<i ==2^i,>=d[a] 没有a的高,还要往上爬
b=p[b][i];
}
if(a == b) //这种情况:b是a的子树
return a;
同一深度的点一起向上爬
//爬树中,原理:拆半查找原理
k = (int)(log(d[b]-1)/log(2));
for(i=k;i>=0;i--)
if(p[a][i] != p[b][i])
{
a=p[a][i];
b=p[b][i];
}
return p[a][0];
完整代码
/*
数据:
1
1 2 3 4
3 5 6 7
6 8 9
7 10 11
10 12 13
*/
#include <cstdio>
#include <cstring>
#include <cmath> //为了使用log()函数
int n; // 总共有n个点
int d[100] = {0};//每个点的深度
int f[100];//每个点的父亲
int p[100][100];
void st(){
int i,j;
memset(p,-1,sizeof(p));
for(i=1;i<=n;i++) // n个点,dp边界
p[i][0]=f[i];
//n个点,理论最深是n,也就是最大有n-1倍祖先,我们算大一点:算成n倍祖先
// 2^j =n --->j=log(n)/log(2)
for(j=1;j<=(int)(log(n)/log(2));j++)
for(i=1;i<=n;i++)
if(p[i][j-1] != -1)// [1] p[i][j-1] != -1 表明可以用自己去更新别人,为什么要有这个判断?
p[i][j] = p[p[i][j-1]][j-1];
}
// 求点a,b的最近公共祖先
int LCA(int a,int b){
/* 先判断是否 d[a] > d[b] ,如果是的话就交换一下(保证 a 的深度小于b,方便下面的操作) */
int i;
if(d[a] > d[b])
{
int tmp =a;
a=b;
b=tmp;
}
/* 转为找同层结点 d[a] <= d[b] */
/* 这种找法 能成功的原因,看折半查找原理*/
int k = (int)(log(d[b]-1)/log(2));//公式 root 点是b点d[b]-1倍祖先
for(i=k;i>=0;i--){
if(d[b]-(1<<i) >=d[a])
b=p[b][i];
}
if(a == b) //这种情况:b是a的子树
return a;
//爬树中,原理:拆半查找原理
k = (int)(log(d[b]-1)/log(2));
for(i=k;i>=0;i--)
if(p[a][i] != p[b][i])
{
a=p[a][i];
b=p[b][i];
}
return p[a][0];
}
int main(){
//太难受了,手动建立树
n=13;
int root =1;
d[root] =1;
f[root] = -1;// [2] 在这里,f[root] =-1 比较好,可以少算很多
f[3]=f[2]=f[4] =root; d[3] = d[2]=d[4]=d[root]+1;
f[5]=f[6]=f[7] =3; d[5] = d[6] =d[7] =d[3]+1;
f[10]=f[11] =7; d[10]=d[11] =d[7]+1;
f[12]=f[13]=10; d[12]=d[13]=d[10]+1;
f[8]=f[9]=6; d[8]=d[9]=d[6]+1;
//预处理
st();
//LCA
int tmp = LCA(9,12);
printf("%d",tmp);
return 0;
}